Появление и распространение инфекционных заболеваний, представляет собой сложный механизм взаимодействующих факторов, таких как окружающая среда, в которой расположены болезнетворные микроорганизмы и организмы, их переносят, а также внутренняя и внешняя динамика населения. Математическое моделирование в эпидемиологии позволяет смоделировать появление и распространение болезнетворных микроорганизмов. Для этого населения делятся на определенные группы лиц, в зависимости от состояния здоровья и уровня распространения возбудителя в популяции. Одной из базовых моделей, которая была успешно исследованной, стала модель Кермак-Маккендрик, построенная в начале 1990-х годов.
Эти модели известны как полигамные модели в эпидемиологии , а также служат в качестве базовых математических моделей, позволяющих понять сложную динамику и основные особенности этих систем. В простейшем случае население делится на две группы: восприимчивых к заболеванию лиц (обозначают, как S), и лиц инфицированных патогеном (обозначают как I). Таким образом, патогенная взаимодействие базируется на феноменологических предположениях, на основе которых построена математическая модель. Для исследования этих моделей используют обычные дифференциальные уравнения (которые являются детерминированными), однако можно рассматривать и стохастические модели (например, модель Гиллеспи). В дальнейшем использовании этих моделей, также описывается количество лиц, выздоровели (обозначают, как R).
Получив возможность моделировать распространение инфекционных патогенов в полигамных моделях, мы можем спрогнозировать различные свойства патогена, например, распространение (общее количество лиц инфицированных от эпидемии) и продолжительность эпидемии. Кроме того, мы получаем возможность понять возможные последствия эпидемии при различных ситуаций, например, каким образом лучше всего проводить вакцинацию населения, при ограниченном количестве вакцин.
SIR модель
SIR модель включает разделение населения на три группы: S — количество лиц восприимчивых к заболеванию, I — количество инфицированных и R — количество лиц, которые выздоровели и имеют иммунитет. Эта модель не является сложной при решении и одновременно позволяет строить распространения многих инфекционных заболеваний, в том числе против кори, эндемического паротита и краснухи.
Для того чтобы, показать, что значение S, I, R меняются со временем (даже если общая численность населения остается неизменной), мы будем обозначать их как функции зависящие от времени S (t), I (t) и R (t). Эти функции будут менять в зависимости от заболевания и популяции, чтобы иметь возможность спрогнозировать возможные вспышки и взять их под контроль.
SIR модель, без учета жизненного цикла населения
Динамика развития эпидемии, например, гриппа, часто гораздо быстрее, чем динамика рождения и смерти населения, поэтому, в простых полигамных моделях жизненный цикл населения достаточно часто опускается. SIR модель без учета жизненного цикла населения (рождения и смерти, или иногда называют демографией) может быть описана следующей системой дифференциальных уравнений:
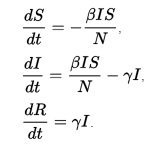
Эта модель впервые была предложена А. Кермак и Андерсоном Греем Маккендрик, особый случай которого называется теорией Кермак-Маккендрик.
Эта система является нелинейной, и нет обобщенного аналитического развязку. Однако, определенные результаты этой модели могут быть получены аналитически.
Во-первых, заметим, что:
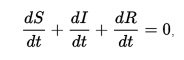
отсюда следует, что:
где N- численность населения, считается постоянной. Следует отметить, что вышеприведенное соотношение означает, что возникает необходимость решать уравнения, для двух из трех переменных.
Во-вторых, следует отметить, что динамика инфекционного заболевания зависит от следующего соотношения:
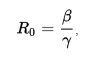
здесь R0— коэффициент распространения инфекции. Это соотношение показывает число новых случаев распространения инфекции, где все лица восприимчивыми к заболеванию. Мы сможем лучше понять эту идею, если обозначим время контакта между лицом и инфекцией Tc=B-1 И время выздоровления Tγ=γ-1. Отсюда следует, что, в среднем, количество контактов зараженного человека с другими людьми, прежде чем она выздоровеет равно Tγ/Tc
Поделив третье дифференциальное уравнение на третье, отделив переменные и проинтегрировав получаем:
где S(0) и R(0) начальные значения восприимчивых к заболеванию и тех, что выздоровели человек соответственно. Таким образом направив t → + ∞ Доля лиц, выздоровели отвечать следующему уравнению:
Это уравнение показывает, что в конце эпидемии, даже если S(0) = 0, Не все особи популяции выздоровели, поэтому должно оставаться определенное число лиц восприимчивых к заболеванию. Это означает, что конец эпидемии вызванный сокращением числа инфицированных людей, а не полной отсутствие восприимчивых к заболеванию лиц. Роль коэффициента распространения инфекции является чрезвычайно важной. Действительно, переписав уравнение изменения количества инфицированных следующим образом:
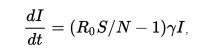
получаем, если:
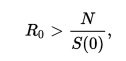
тогда
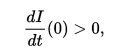
то есть произойдет вспышка эпидемии с ростом числа инфицированных лиц. И наоборот, если
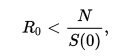
тогда
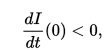
то есть, независимо от исходного количества восприимчивых к заболеванию лиц, болезнь никогда не сможет вызвать вспышку эпидемии.
Сила действия инфекции
Обратите внимание, что приведенная ранее функция:
которая моделирует скорость изменения восприимчивых к заболеванию лиц на инфицированных является силой действия инфекции. Однако для многих групп инфекционных заболеваний, более реалистично рассматривать силу действия инфекции, которая зависит не от числа инфицированных, а от доли этих лиц относительно всего населения:
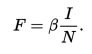
Аналитическое решение для SIR модели
В 2014 году Harko T. и др. получили точное аналитическое решение SIR модели. В модели без учета жизненного цикла населения, для S (u) = S (t), то есть обеспечивается соответствие временной параметризации
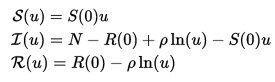
для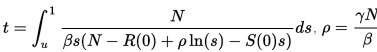 
С начальными условиями 
где υΤ удовлетворяет Ι (υΤ) = 0. Из уравнения, описанного выше, для R∞ следует, что, 
если 
